TI图形计算器在数学教学中的运用探寻

主题词 TI图形计算器 数学教学 探索发现

TI图形计算器是一种“掌上电脑”，其内部设置了功能强大的数学教学专用软件，如计算机符号代数系统、几何绘图系统、数据处理系统等，还具有程序编辑功能．与TI图形计算器相配合的“以计算器为基础的实验室”（CBL）等数据采集装置，可用来收集与处理各种数据，如位移、速度、温度、声音、光、力、电等等，并能方便地传输给图形计算器，进而用数学手段加以分析处理．

我校开展对TI图形计算器的研究，已近三年的时间．在过去的两年里，我作为此课题的成员之一，在高一《全日制普通高级中学教科书（试验修订本）·数学·第一册（上）》第二章《函数》和第三章《数列》，《全日制普通高级中学教科书（试验修订本）·数学·第一册（下）》第四章《三角函数》，高二《全日制普通高级中学教科书（试验修订本）·数学·第二册（上）》第七章《直线和圆的方程》和第八章《圆锥曲线方程》等章节的教学中，进行了师生共同探究，启发学生去“发现”的师生互动式的教学模式．探究什么？又去“发现”什么？探究的最终目的是什么？……这种教学模式是如何具体操作的，实践下来的效果又如何呢？可以这样说，将TI图形计算器引入到高中数学课堂，为培养学生的创新精神和实践能力拓开了一片更加广阔的天地，给学生营造出了一个真正属于自己的、展现学生个性的大舞台．下面我就简单谈一谈在数学课堂教学中利用图形计算器，使学生对各种自然现象和科学规律进行观察、思考和研究，使他们亲历各种数理知识的形成以及建立模型、探索规律的过程．

一、在课堂教学中引入TI图形计算器打破了以教师为中心的传统观念，有利于突出学生在教学过程中的主体地位

在教学过程中，要想改变以往那种以教师为中心的传统观念就必须加强学生在教学这一师生双边活动中的主体参与，让每一个学生都有动脉、动手、动嘴的机会，注重学生在认知过程中的主体作用．所以课堂上要给学生创设暴露思维过程的情境，使他们大胆地想、充分地问、多方位地交流，教师要在教学活动中从一个知识的传播者自觉转变为与学生一起发现问题、探讨问题、解决问题的组织者、引导者．而TI图形计算器恰恰在这方面为师生营造了他们共同需要的氛围．

例如在复习《指数函数的图象》时，我让学生先作出几组函数图象，然后观察函数图象的特点，并总结每一组函数图象之间的关系．我在黑板上写的其中一组函数是y = 2^x与y =－2^x，学生利用TI图形计算器作出图象（如图1），

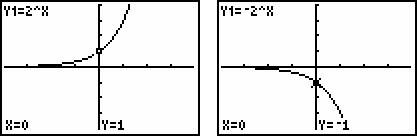
图1

一位学生在输入解析式时，输成了y = (－2) ^x， 好一会儿，计算器也没有画出所要的图象，而是一些散点（如图2），

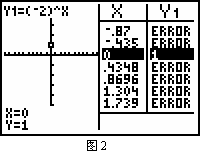
这位学生让其他同学检查也没有发现问题出在哪里，怀疑是计算器出了问题．我发现是由于他的解析式输入错了，便要求他仔细对照黑板上的解析式，自己找出问题．他找出问题作出函数图象后，我问他：“你知道为什么计算器画不出你输入的解析式的图象吗？”“指数函数的底数a必须大于0且不等于1．”他不假思索地回答．我又追问：“你知道为什么在指数函数的定义中要做如此规定吗？” 他诧异地望着我摇摇头，同组的其他同学也不知如何回答．我将y = (－2)^x写在黑板上，让全班学生讨论指数函数的底数a为什么必须大于0且不等于1．学生们热烈地讨论起来，不一会儿就有同学举起手，当那个粗心的学生也举手时，我叫起他，教室里安静了，他说：y = (－2)^x不满足对一切实数x都有意义，所以计算器画不出它的图象．我表扬他积极思考，又再次强调指数函数、对数函数中的底数a都必须大于0且不等于1．

在这一最基本概念再次得到澄清的过程中，同学们通过出现问题、检查问题、改正问题并反思问题，最终通过同学之间的讨论解决问题，使自己对这一最基本概念的认识进一步加深．而这一次的理解之所以深刻都是缘于他们亲自尝试失败的结果．

二、在课堂教学中引入TI图形计算器为培养学生的创新思维能力提供了得天独厚的条件

中学数学教学是思维活动的教学，对学生创新思维能力的培养是中学数学教学的核心．在数学课堂教学中引入TI图形计算器，为培养学生的创新思维能力提供了得天独厚的条件．

（一）．TI图形计算器为学生获取信息、处理问题提供了新途径、新方法

以往的计算机辅助教学多以教师创设问题情境，学生猜想，进而由教师利用计算机演示，对同学们的猜想加以验证的方式为主．这种做法虽然克服了传统教学手段无法表现动态效果的缺陷，使抽象的数学知识更加直观，但教学过程仍然是以教师演示学生观看为主，学生仍然处于一种被动地接受的地位．他们不知道老师的课件是如何制作成的，他们的心往往被一种新奇感占据．而TI图形计算器则弥补了这一不足，真正使数学教学活动从以学生看教师表演的方式转变为让每个学生都有机会表演给大家看、讲给大家听的方式，真正使学生成为了教学活动的主人，使学生有机会表现自我，也使数学教学走向了真正的意义上的以人为本、张扬个性的层面，而且为学生获取信息、处理问题提供了新途径和新方法．

例如在复习《对数函数的图象和性质》一节课时我给学生出了一道讨论题：

题目：若log_m5>log_n5（m, n>0且m≠1, n≠1），讨论m, n, 0, 1的大小关系．

在以前的教学中我都是先举一例：若log_m5>log_n5（m, n>0且m≠1, n≠1），比较m, n的大小，再让学生做第二问log_m5>log_n5（m, n>0且m≠1, n≠1），比较m, n,0, 1的大小．这一次我直接给出第二问，让学生自己动脑、动手做这道题，然后与本组同学讨论交流，把最后总结好的解题思路和详细解答过程讲给全班同学听．

我在备课时已准备了两种方法，但出乎我意料的是一位数学成绩并不算好的学生在我出完例题不到5分钟便作出了正确答案，更令我惊讶的是她的方法竟是我未曾想到的．她的具体做法如下：

首先利用TI图形计算器画出函数y=log_m5的图象，如图3所示．然后根据图象确定m, n, 0, 1的大小．由图可知：

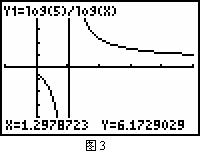
（1）当0< x <1时，因为y=log_x5为减函数，又由y=log_m5> y=log_n5，得0<m<n<1

（2）当x>1时，y=log_x5为减函数，由y=log_m5> y=log_n5，得0<1<m<n

（3）根据图象，当log_m5>0，log_n5<0，得0<n<1<m

此外还可以通过TI列表的方法，观察出当0<x<1、x = 1和x>1时，函数值及其的变化，如图4

从上面的解题过程可以看出结合函数y=log_x5的图象，m,n,0,1的大小关系竟是如此直观，而这个函数是我们在以往的教学中不曾涉及的，当然更不会去关注这些初等函数以外的函数的图象．但是有了TI图形计算器，同学们获取知识的渠道又多了一条，他们认识了以往教师不可能教、自己不可能认识的函数图象，并用它有效地解决了问题．所以说TI图形计算器拓宽了学生的认知领域，为学生获取信息、处理问题提供了新的途径和新方法．

（二）．TI图形计算器为师生进行探索、发现创设了有利的情境

仔细分析一下函数y=log_x5不难发现，由于log_x5=，所以，函数y=log_x5是由y =和u(x)=log₅x复合而成的 ，因为y关于u在（– ∞, 0）和（0, + ∞）上都为减函数，而u关于x在（0, + ∞）上又为增函数，所以y关于x在（0, +∞）上是减函数．这一点在教师的引导下根据复合函数单调性的判断方法学生是完全可以想到的．

由此可见，TI图形计算器为师生共同进行探索和发现创设了有利的情境，只要教师善于捕捉学生中可贵的创新的闪光点，并能及时加以引导，就能在课堂教学中创设出培养学生的创造性思维的契机和素材．

可以说是上面的开放性的问题为学生创设了一个有利于解放思维、讨论交流的机会，是TI图形计算器为师生思维过程的双向暴露提供了可能．在教学过程中，通过学生的主动参与、合作讨论，使学生真正感受到了自己的表达见解、行为方式得到了最大限度的尊重，他们的创造性思维能力和与人协作的能力都得到了培养．

参考文献

《普通高级中学实验教科书.信息技术整合本》教师汇率参考资料 人教社

陶维林： 《用新课标理念设计一堂课的教学》.数学通报. 2004.8