一、问题的背景：
当前，随着经济发展改革的深入，在商品市场上，消费者购买住房、汽车等价值较高的商品时，为缓解资金的暂缺，消费者可向银行申请贷款，采取分期付款方式。高一数学新教材上册第四章数列的研究性学习内容中介绍了分期付款的一个数学模型，既"等额本息还款法"，它是一个等比数列的问题，这个模型非常有应用价值。在国内外商品交易的分期付款中被广泛的使用。那么；分期付款是否还有其它还款方法吗？带着疑问，我与学生到几个银行进行一番调查，了解到；分期付款还有另一种方法，即"等额本金付款法"，此方法，在国内外商品交易分期付款中也普遍被使用。经研究，我发现此问题是一个等差数列的数学模型，两种分期付款方法，两种数学模型又如此的对称；使我意识到，这不是偶然的巧合，它正说明了，数列知识在金融领域有着广泛的应用，这也大大激发了我对这个问题深入研究的热情和兴趣..........。
下面我就介绍一下;在课堂上，我是怎样通过探究式学习，引导学生来完成 "等额本金还款法"的建模过程和用TI图形计算器编程解决计算问题的方法。
二、活动设计的目的：
通过对"等额本金"还款法的研究过程：
1.使学生清楚的看到课本中数学知识（数列）在金融和社会生各个领域中应用的鲜明的背景。激发他们对学习数学的兴趣和动力。
2.提高学生归纳、总结问题能力；掌握数学建模的思想方法。
3.使学生学会利用现代技术TI图形计算器编程解决计算问题，培养创新能力。
4.突破中学数学教学中的难点──应用问题、复杂和烦琐的计算。
5.培养学生的合作精神和合作意识，使学生在合作中体会到合作的重要性、有效性。
三、活动的过程：
探究性活动课包括教师的教学设计活动和学生的探究活动两个方面。教学设计活动一般包括确定主题、选择任务、规划过程、提供资源、评估和结论五个环节，学生的探究活动则主要包括审视主题、明确分工、过程设计、实施探究和发表成果五个环节。
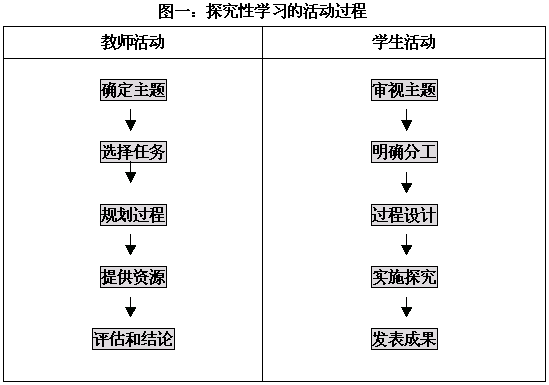
教师的设计包括如下几个方面：
1、 确定主题。确定主题的目的是为了使学生明白将要通过该问题的讨论明确学习什么和开展这项学习活动的目的意义。主题的确定要考虑到学生的学习基础和学习需要。
2、 设计任务。任务设计是主题的进一步具体化，是任务驱动式学习的一个必要步骤。
3、 向学生提供探究路径。具体的、可操作的研究路径可减少学生的研究成本。
4、评估和结论。教师应对讨论式学习活动进行评估和测评来考察实际效果，以及对整个活动进行反思，对活动的成果进行拓展和推广。
学生的活动内容包括如下几个方面：
1、根据主题和任务，进行分工协作，明确各自的任务，通过讨论、互相交流、共同对问题进行探究。
2、对老师提供的资源和自己收集掌握的资料、信息进行分析、处理和重组，创造新的思想，得出新的结论。发表自己的探究结论和成果。
下面以教学中开发的分期付款中"等额本金还款法"问题为例，来进一步具体说明探究式学习和应用TI图形计算器的活动的过程。
课题名称：在探究性活动课上TI图形计算器的应用
课题来源：商品交易过程中的分期付款中国金价问题
活动时间：一个课时。
课室环境：普通教室，6～8人分为一个小组。
课堂活动：
1）教师用5分钟安排（同学们已进行过多次，安排的时间还可以缩短，尽量把课堂时间还给学生！），其中3分钟介绍讨论式学习活动的要求，2分钟安排各个小组的任务。与此同时，向每一位同学推荐活动计划。
2）同学们分组完成探究任务。在探究过程中，鼓励学生相互交流与合作。
3）用10分种时间请部分学生在班上介绍自己的探究结果和成果，供大家分享。
四、 活动结果及分析
从教师的活动方面来说，讨论式学习是探究式学习模式与当前我们开展的研究性学习模式有不同之处，前者的研究主题、任务、路径和资源都由教师提供，而后者从课题的选择、研究的设计、参考文献的查找等都由学生自主地完成，所以，探究性模式是一种由教师"控制"程度相对较高的研究，适合于目标较为明确的课堂教学。
从学生的活动方面来说，开展探究式学习，目的是为了锻炼学生的实践能力和解决问题的能力，方式主要是学生利用所学课本知识和自己了解到的及教师提供的资料和信息自主地去完成，学生们进行了交流与合作，并以小组为单位提交了书面结果。学生对这些信息进行了归纳总结，说明同学们完成老师安排的任务质量还是较高的。因此，开展的探究式学习与我们当前开展的研究性学习在培养学生创新性能力的宗旨上是一致的。
五、收获体会
通过课堂实践,自己感觉到这种学习方式有以下一些突出的优点：
1、在课堂教学中开展探究式学习,有利于知识的积累和能力的提高。首先，在老师的周密设计下，学习目标是具体的、明确的。其次，带着主题和任务的分析问题，拓宽了学生的视野及知识面。再次，以社会内容为课题来源的活动，使学生明确知识来源于社会,又服务于社会。
2、在课堂上遇到计算量大、计算烦琐、容易出错等问题，运用TI图形计算器解决了这个问题，是一种创新思维。也使学生看到了用TI图形计算器，在学习和解决实际问题的重要性和实效性，激发了学习兴趣。
六、活动设计要点
1、本内容以教材（数列内容）为核心向外扩散，其目的是为了"一举两得"，既有利于学生课本知识的掌握，又有利于学生实践能力和探究能力的提高。
2、学习方式上既要发挥学生的主动性，由学生自主地完成探究过程，又要发挥教师的创造性，这一点特别重要。因为在评价传统教学没有发挥学生主动性的过程中，我们有可能走向另一个极端，即排斥教师在教学中的作用。探究式学习需要教师课前精密的设计，只有这样，才能使我们的最有效地利用课堂教学时间，"让教师做最好的导演，让学生做最好的演员"，这就是探究式学习方式的要领。
3、评估旨在反思，而不要流于外在的形式。探究式学习需要评估来考察学生结论和结果的创造性和正确性，需要对学习的内容和过程进行反思。我认为，最重要的在于学生在学习过程中真正的发挥了自主性，进行了创造性的思考。
七、参考文献：
1、 普通高级中学实验教课书（信息技术整合本）数学第一册（上）
2、 现行高中数学新教材课本上册;
3、 中国人民银行、工商行、中国建设银行个人金融产品商业贷款资料。
4、 美国德州仪器公司TI计算器参考手册。
附件：课题内容：
在探究式学习活动课上TI图形计算器的应用
──分期付款中等额本金还款法
北京育才学校 刘玉德
一、 问题提出
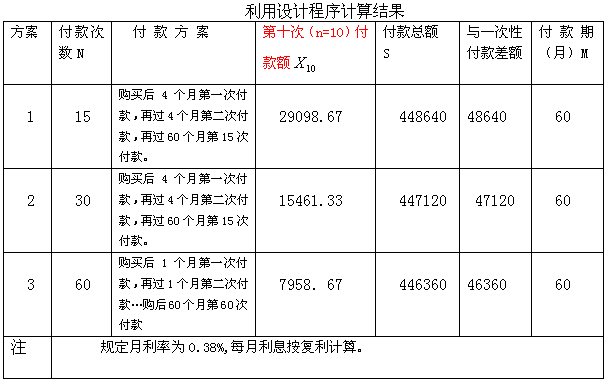
当前，随着经济发展改革的深入，在商品市场上，消费者购买住房、汽车等价值商较高的商品时，为缓解资金的暂缺，消费者可向银行申请贷款，采取分期付款方式。如，购买一套价值为400000元的住房，五年（也有3年、4年，10年等）内将全部款付清。假设有以下几种付款方案：
方案1：分15次付款( 购房后每4个月付款一次 )，5年付清（60个月）。
方案2：分30次付款 ( 购房后每2个月付款一次 )，5年付清（60个月）。
方案3：分60次付款( 购房后每1个月付款一次 )，5年付清（60个月）。
（假如你的家庭意欲采取分期付款购买住房或轿车，你能运用所学知识对几种付款方式进行权衡吗？）
资料：分期付款的有关情况和规定（等额本金还款法）：
1、 贷款人每次等额偿还本金，
2、 贷款利息随所还本金逐次递减。
消费者从上面选择付款方案时，需要知道几种方案中每期应付款多少，付款总额为多少，这样才便于比较、权衡。确定自己按那种方案购买住房。。
下面我们研究一下，采用方案2，每期应付款各为多少，五年总共应付款又是多少？，
二、 研究过程
1、每期还款额的研究
等额本金还款法原则：每期还款分两部分，既本金和利息，每期还款的本金都相等，利息随所还本金逐次递减。
因此，每期还款额 = 每期还款本金 + 每期还款利息
又因为每期还款的本金都相等，所以采用方案2：（如果月利率取0.38℅）
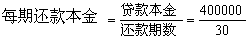
每期还款利息 =（贷款本金 - 累计已还本金） 月利率 2 （每两个月还付一次）也就是：
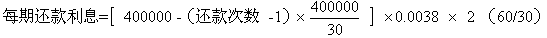
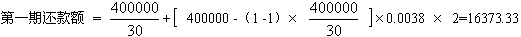
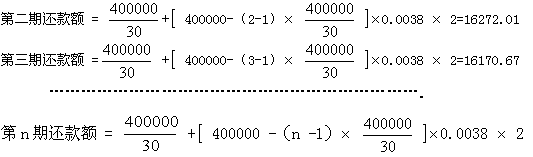
设每期还款额为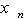
，贷款本金额为A，还清款总月数为M，还清款次数总和为N，月利率为P，还款次数为n,（A、M、N是常数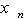，和n是变数
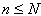，归纳后得出（这是不完全归纳，应该用数学归纳法证明之，证略）：
每期还款额的数学模型为
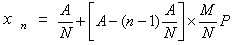（1）
2、分期付款总额的研究
由模型（1）可知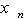是一个首项为
公差为
的等差数列（证略）。由公差小于零可知，此数列是一个单调递减的等差数列
求得第n次付款的前n项和为
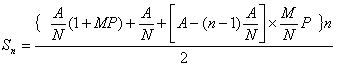
化简后前n次付款总额的数学模型为：
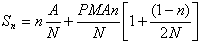（2）
在选择几种方案进行比较、权衡时，一般要利用上述两个公式计算以下每期付款和付款总额。由于计算量之大，公式子的吭长，总令人望而生畏，如果用TI图形计算器设计计算程序后，可以避开繁琐的公式计算，时间计算器只要输入数据，就可以轻松得出各种方案的答案。
三、程序设计与计算过程：
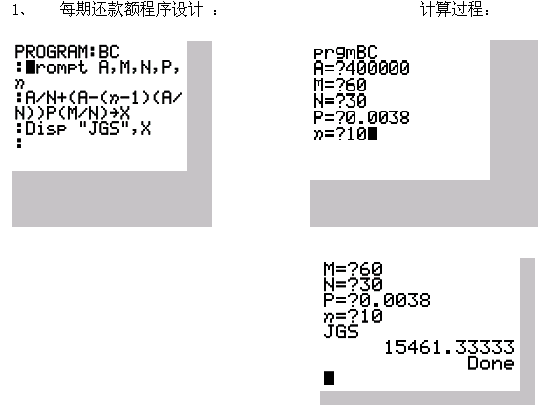
计算得第十期付款额为15461.333元。(也可以选择其它付款方案进行各期付款额的计算)
计算五年（60月）还款总额为447120元。（其它付款方案结果均可以由该程序计算得到）
四、总结与反思
分期付款问题的研究分两个过程。
1、每期付款额和各期付款总额数学模型建立，体现数学的一种建模思想。（上述两个模型严格说要用数学归纳法证明，这里证略）。
2、用TI图形计算器编程进行各种方案计算，体现数学的一种计算方法。
两者的统一是数学研究问题的完整过程。
在计算出结果后，消费者会对自己如何购买住房（或汽车）作出正确的决择。
在研究"等额本金还款法"这个问题的过程中，TI图形计算器为我们师生解决问题提供了强有力的支持。课堂上，两个数学模型建立后，学生们不满足直接的利用计算器对模型进行计算，在发现计算烦琐、麻烦、容易出错（必须记住数学模型）后，在老师的引导下，很多学生又提出编程，自己设计程序解决这个问题要求，而编程本身就是一种创造，学生的提法就是一种创新思维。因此；我们可以利用TI图形计算器随心所欲的探究各类与数学有关的问题。
一位国际知名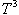
在职教师发展计划的主要创建者，美国俄亥俄洲立大学数学系B.K.Waits教授曾经自信地说过："我相信图形计算器──被有强烈求知欲望的学生和有见识的教师所使用；对今天积极的数学教学的改革来说是最伟大的力量"。我相信，随着TI图形计算器在课堂上使用的深入和普及，必定对当前数学教学的改革产生不可估量的积极影响。