那么，怎样使用技术来改进学生的数学学习方式？技术支持下的数学学习又有什么特点呢？ Collis早在1996年就指出，最佳的应用信息技术的起步方案，是教师从课堂的实践经验中，辨别出应用传统教学模式施教而效果欠佳的项目，尝试利用信息技术的协助寻找可行方案，解决部分或全部的困难。
本课例是TI技术支持下对圆锥曲线若干（射影）性质的研究性学习，期望能引起各位老师对技术支持下的数学探索的再思考，权作抛砖引玉。
教学过程：
1．创设情境 问题由学生提出：
问题是研究性学习的核心，能否提出对学生具有挑战性和吸引力的问题并使学生产生问题意识，是进行研究性学习的关键。美国教育家布鲁巴克认为：“最精湛的教育艺术，遵循的最高准则就是学生自己提出问题。”
T：美国著名数学家哈尔莫斯说“问题是数学的心脏”。从推动科学进步和个人终身发展来看，独立发现和提出问题往往显得非常重要。那么，怎样独立发现和提出问题呢？一条重要的途径就是从当前研究的典型问题出发，应用恰当的（数学）方法挖掘、发现新的问题。
当前问题（ppt1）：已知线段AB是抛物线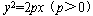
的焦点弦，F是焦点，准线L与x轴交于点E，作BN⊥L于N。求证：直线AN过抛物线的顶点O；∠AEF＝∠BEF。
能将上述问题进行推广与引申吗？（激励学生发现问题的意识和提出问题的勇气，希望学生能自己发现并提出一些猜想，并用技术检验自己的猜想）
：在椭圆和双曲线中这些结论应该也是成立的，即有：
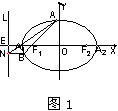
猜想1：如图1，设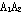
是椭圆的长轴，AB是过椭圆左焦点F的弦，BN∥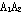交椭圆的左准线L于N点。则直线AN过椭圆的左顶点；∠AEF＝∠BEF 。
猜想2：如图2，设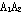是双曲线的实轴，AB是过双曲线右焦点F的弦，BN∥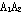交双曲线的右准线L于N点。则AN过双曲线的左顶点；∠AEF＝∠BEF 。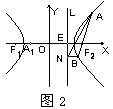
T：好！“千古数学一大猜。”（华罗庚）没有大胆的猜想，就不会有伟大的发现。猜想总是正确的吗？（学生：不是！）由于两个猜想的相似性和时间的关系，我们不平均使用力量，建议同学们对猜想1进行实验与讨论。
2．动手实验 检验、修正猜想：
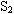：猜想1的第一个结论是错的，但直线AN与直线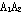的交点Q仍是定点。利用TI图形计算器中几何画板的度量功能，分别测算出E、Q、F的坐标，当拖动点A时，可以发现Q 是线段EF的中点（如图3）。
：我同意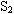的观点，我是这样检验的：分别测算出线段EQ、FQ的长度，当拖动点A时，线段EQ、FQ的长度总是相当的，所以Q 是线段EF的中点。
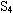：当拖动点A时，可以发现Q是定点，利用特殊化思想，当AB⊥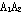时，由椭圆的对称性和三角形中位线性质知线段FQ是线段BN的一半，而此时|BN|＝|EF|，所以Q 是线段EF的中点（如图4）。
面对这几个同学有理有据、形象直观的“展示”，同学们报以热烈的掌声，此情此景更激发了学生探索发现的欲望和动机。
T：三位同学在“TI技术”的支持下，以不同的方式（多重联系表示）得到了同样的结论，特别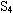同学在特殊化思想指导下，利用椭圆的对称性巧妙地发现了Q 是线段EF的中点，可谓“巧用对称性，曲径变坦途”。这一切很值得大家细细品味。
3．理性思考 逻辑证明：
“证明是数学的灵魂”（黑格尔）。猜想不等于证明，在数学的探索性活动中，不能把“结论”仅停止于猜想阶段，如有可能要力争给出它的逻辑证明。由于学生自己提出猜想，并在“技术”的支持下改进了猜想，自然就会有追求证明的渴望，因而此时的数学教学最富有吸引力，莫错良机。
T：通过实验改进了猜想，这能代表探索、研究已经结束了吗？（同学们附和：不能！），是的！证明或否定猜想是科学发现中不可或缺的关键环节。那么，能给出证明呢？
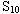
：由于这个证明中并没有用到椭圆离心率的大小，因此，这个证明也适用于双曲线和抛物线，即这是圆锥曲线的一个共同性质。其实，抛物线的顶点O就是线段EF的中点，这个推广是合情合理的。
T：妙极了！真是得来全不费功夫！
根据圆锥曲线的第二定义并巧妙地应用平面几何性质，一举搞定抛物线、椭圆、双曲线中的相关问题，可谓“一石三鸟”收获丰。这是简单与严谨的统一，这是一个激动人心的优美解！
同学们被证明中所体现出的简单美、和谐美与统一美深深地震撼了。
T：回顾前面的探索，我们经历了“类比猜想──动手实验──否定猜想──改进猜想──证实猜想”的过程，这是探索数学规律与发现数学本质的基本过程。其中，错误与挫折是在所难免的，我们不仅不能否定同学的做法，相反应该非常感谢他给我们提出了一个极富挑战性的问题，是他的猜想引起了我们的思考，锻炼了我们的思维。
4．拓展性探索：
探索奥秘是人的天性。以罗杰斯为代表的人本主义学习理论认为，人天生就有寻求真理、探索奥秘和创造的欲望以及自我主动学习的潜能。学习过程就是这种潜能自主发挥的过程。在适宜的环境下，个人所具有的学习、发现、丰富知识与经验的潜能是能够最大限度地释放出来的。
T：对于同学提出的猜想我们都已经解决了吗？
：关于角的结论还没有研究。我想应该把问题一般化，即线段AB是圆锥曲线的任意弦，并且线段AB与它的焦点所在的对称轴交于M点，该轴上是否存在一点E，使∠AEM＝∠BEM ？
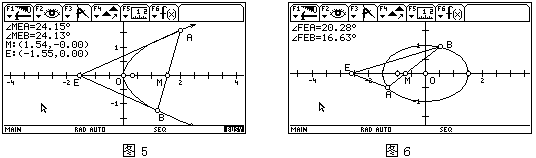
：对于抛物线来说，这个点是存在的。设E是抛物线对称轴上的点，度量∠AEM、∠BEM，慢慢拖动点E时，发现当点E和点M几乎关于抛物线的顶点对称时，近似地有∠AEM＝∠BEM（如图5）。若改变做法：作点M关于顶点的对称点E，再度量∠AEM、∠BEM，当拖动点A时，总有∠AEM＝∠BEM（图略）。
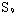：这个结论在椭圆并不成立，我也是作点M关于椭圆左顶点的对称点E，再度量∠AEM、∠BEM，当拖动点A时，发现∠AEM≠∠BEM。如果在x轴上任取一点E，并度量∠AEM、∠BEM，当拖动点E时，仍然是∠AEM≠∠BEM（如图6）。
此时一片哗然，学生惊奇地发现实验的结果竟与他们的猜想是极不协调的。
在科学发现中，错误和失败不仅是难免的，也是我们所需要的，很多情况下，真理来自错误，成功源自失败。英国心理学家贝恩布里就说过：“差错人皆有之，作为教师，对学生的错误不加以利用是不可原谅的。”教师的责任就是帮助学生“尝试失败，并从中总结经验和教训，逐渐学会由失败走向成功。”（郝澎）当学生陷入困境时，教师要重新点燃学生思维的火花，使他们树立探索发现的勇气和信心。
T：真的会是这样吗？同是圆锥曲线，为什么在抛物线中成立的结论却在椭圆不成立了呢？在探索与发现中即要“大胆假设”又要“小心求证”。能在同学的实验中有所发现吗？
同学们带着极大的好奇心开始了新的探索实验。很快就有人喊道：慢慢拖动点E，有相等的时候！
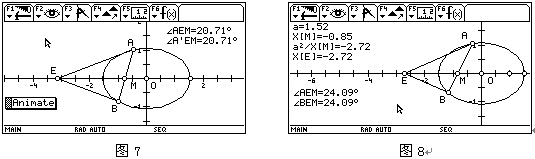
：我这是一个“本末倒置”的实验：作线段AE关于x轴的对称线段交椭圆于B点，线段AB交x轴于M点，当拖动点A时，总有∠AEM＝∠BEM（如图7）。这说明对于过定点M的任意弦AB，x轴上存在一点E使∠AEM＝∠BEM。
T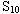：同学的实验演示，直观、形象地说明这样的“点”是存在的。那么，这个点的本质到底是什么呢？怎样确定它坐标呢？
S2：我的想法是这样的，若AB是经过椭圆焦点F的弦，E是对应的准线与x轴的交点，经过测算∠AEF＝∠BEF，当改变椭圆两轴的大小及拖动点A时，这个结论还成立。而此时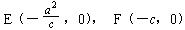
，显然有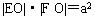
（a是椭圆的半长轴长，c是椭圆的半焦距长）。所以我猜想：设椭圆的弦AB与x轴交于点
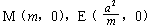是x轴上的点，则∠AEF＝∠BEF。经过实验，猜想成立（如图8）。
T：太棒了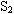！同学以退求进，以实实在在的例子告诉我们E与M的关系，能证明吗？
学生们喊道：用斜率。
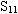：这只要在已知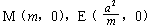的条件下，计算直线AE与BE的斜率和为零，即可；反过来，设
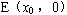是x轴上的点，并且∠AEF＝∠BEF，则可由直线AE与BE的斜率和为零求得
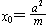。也就是说，若椭圆的弦AB 与x轴交于点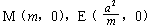是x轴上的点，则∠AEF＝∠BEF等价于。
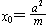T：好极了！他不仅提供了问题解决的方案，而且将探索研究的结果作了简单总结和概括。
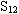：应补充条件m≠0。
教师与众学生：啊！的确如此，否则，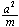
就无意义了。
T：但是，这是不是有一点令人遗憾呀！为什么出现这不和谐的“音符”（点）呢？
全体同学再一次投入到激烈的讨论和探索活动中去。又举手了。
：点M由左向右渐渐无限靠近原点时，点E由右向左逐渐趋向负无穷远，E可看作x轴负方向上的无穷远点，此时射线AE、BE平行于x轴，它们与x轴所成的角都是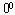
，即，仍然有∠AEF＝∠BEF，（如图9）。
：当点M由左向右“越过”原点时，E就会从x轴正方向的无穷远点处返回来。
T：妙！实在是妙！在x轴上“虚拟”一个无穷远点（E），把x轴（直线）看作是封闭的“圈”（半径无穷大的圆），矛盾的结论又和谐统一了，这真是“此时无穷胜有穷，道是无情却有情（情理、道理）！”
此时学生都惊叹于圆锥曲线的统一性、奇异性、和谐性，被数学的内在美所震撼，他们的探索精神、创新精神也得到了淋漓尽致的发挥。从失败走向成功，他们体验到了探索中的艰辛与创新成功的喜悦，这有利于形成正确的数学观和创新意识及科学精神。
5．探索无止境 再攀高峰：
T：愉快的时光总是短暂的。请同学们从探索到的结论、探索方法（数学思维方法）及情感体验等方面对本节课进行小结与交流。
学生发言积极踊跃，就在部分同学陶醉于已有的成果时又有学生发现了新的问题：
：我认为，若过点E作L⊥x轴，作BN⊥L于N，则AN平分线段EM。
：其实还可以讨论，如果AB不是经过椭圆长轴上的定点M的弦，而是经过椭圆短轴上的定点M的弦，那么，在椭圆短轴（所在直线）上是否也存在这样的点E呢？
：假设点M不在椭圆的内部，而是在椭圆的外部，特别地，点M是任意点时又会怎样呢？
英国科学家波普尔说：“科学和知识的增长永远始于问题，终于问题──越来越深化的问题，越来越能启发新问题的问题”。问题是不断发现的，原问题的解决，并不意味着探索的终结，而是导致新的更高层次问题的产生。正是在这个不断的探索发现过程中，学生的思维能力在不断发展，探索精神在不断提升。
T：很好！新的问题又在等待着我们，上述问题有较高的价值，但更具挑战性。同学们，学习的过程是一个探索、创造的过程，“惟有创造才是欢乐。”（罗曼·罗兰） 让我们的学习充满创造与欢乐吧！
作业：1 证明本节课所发现的结论；
2 就感兴趣的问题继续探索研究，并写出你的研究报告；
3 就本节课的探索与体验写一篇小作文
教学后记：
数学不只是逻辑，还有实验。TI图形计算器能为学生创设一个理想的“多重联系表示”的几何实验环境。学生在作图、度量、测算、变换等实验活动中，摆脱了繁琐的不可靠的纸笔环境，用更多的时间研究、思考问题。特别是学生的猜想与实验结果的不一致性，能激发学生的好奇心（惊奇性），随着重新探索，学生会从活动中得到一些更有益的反馈，这样的直接反馈比来自老师的反馈更为有效，在多次实验探索后，学生会感到有证明的必要，而证明的逻辑思路多半会在实验活动中产生。这种“做”数学的实验活动不仅使学生亲身体验了数学规律的发现与发展的过程，而且，更为重要的是改变了学生的数学观念：数学不再是枯燥、乏味的公理、定理和形式化证明的简单集合，而是动态的、生动活泼的探索发现过程。
在这节课上，学生多次根据动态的图形和测量的符号表示大胆猜想、发现圆锥曲线中所蕴涵的数学本质，学生高水平的、深层次的数学思维活动得到了TI技术的有力支持。如果用“多元多维”的观点观察课堂，我们发现，学生不再仅凭直觉来分析，而能以数学的观点来思考。正如福斯纳特（Fosnot，C。T。）所描述的：学生与教师之间、学生与学生之间、学生与学习对象之间的相互作用宛如一曲交响乐，时而和谐，时而激励地冲突，在互动中体现探索与交流。
当学生在“问题串”的引导下进行了一系列观察、实验、猜想后，要及时将他们的发现理性升华。发现结论提出猜想，并不代表实验、探索的结束，还要有“数学化”的过程。证明或否定猜想是科学发现中不可或缺的关键环节。要让学生知道，在数学中只有通过逻辑证明而得出的命题才是数学真理。数学要猜想，但不能止于猜想；数学要实验，但不能没有“数学化”。数学教学提倡“返璞”但更要“归真”，没有“归真”的“返璞”只能算是一种“经验”或“常识”。“科学是常识的精微化”，所以，数学教学必须要有“数学化”的过程。当然，有些问题在课堂上能否马上证实并不重要（但要让学生清楚必须有“证实”），在新的教学理念下，我们认为，课堂教学重要的是埋下一颗探索、创新的种子。至于猜想的证明，按高斯或爱因斯坦的话说，不过是一种补行的油價手续了。
显然，本节课中TI技术已不仅仅是教学的辅助工具,它已成为学生认知的强大工具。我们坚信TI教育技术和其它信息技术必将成为“开发和释放人的创造潜能的发动机”。
参考文献：
1． 课题组 （章建跃执笔）。中学数学课程教材与信息技术整合的思考[J]。课程·教材·教法，2002，（10）
2． 郭立昌 图形计算器与中学数学创新教育[J].数学教育学报,2001,10(4)
3． 康 杰 图形计算器在中学数学探究性活动中的应用[J].数学教育学报,2002,11(2)
4． 郝 澎 研究性学习的教学研究[J]。中学数学教学参考，2003，（1，2）
5． 王芝平等 直线方程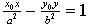
的几何意义[J]。数学通报，2002，（11）
注：本文是根据笔者在4月9日全市“TI技术与探究性学”研讨会上所作的公开课改写而成。