化归思想及其应用

在中学数学中，化归不仅是一种重要的解题思想，也是一种最基本的思维策略。所谓的化归思想方法，就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化，进而达到解决的一种方法。一般总是将复杂问题通过变换转化为简单问题；将难解的问题通过变换转化为容易求解的问题；将未解决的问题通过变换转化为已解决的问题。总之，化归在数学解题中几乎无处不在，化归的基本功能是：生疏化成熟悉，复杂化成简单，抽象化成直观，含糊化成明朗。说到底，化归的实质就是以运动变化发展的观点，以及事物之间相互联系，相互制约的观点看待问题，善于对所要解决的问题进行变换转化，使问题得以解决。这也是辩证唯物主义的基本观点。

匈牙利著名数学家罗莎·彼得在他的名著《无穷的玩艺》中，通过一个十分生动而有趣的笑话，来说明数学家是如何用化归的思想方法来解题的。有人提出了这样一个问题："假设在你面前有煤气灶，水龙头、水壶和火柴，你想烧开水，应当怎样去做？"对此，某人回答说："在壶中灌上水，点燃煤气，再把壶放在煤气灶上。"提问者肯定了这一回答，但是，他又追问道："如果其他的条件都没有变化，只是水壶中已经有了足够的水，那么你又应该怎样去做？"这时被提问者一定会大声而有把握地回答说："点燃煤气，再把水壶放上去。"但是更完善的回答应该是这样的："只有物理学家才会按照刚才所说的办法去做，而数学家却会回答：'只须把水壶中的水倒掉，问题就化归为前面所说的问题了'"。

"把水倒掉"，这就是化归，这就是数学家常用的方法。翻开数学发展的史册，这样的例子不胜枚举，著名的哥尼斯堡七桥问题便是一个精彩的例证。大数学家欧拉解决这一问题的思维程序是：

这是化归问题一个很好的应用，由此我们容易归纳出化归思想方法的思维模式：

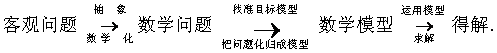
可见解题能力的强弱在于：1、有敏锐的洞察能力，才能找准目标模型，2、有较强的化归能力，才能有效地把问题转化为目标模型，至于运用模型的内部规律求解就比较容易了。

在中学数学中，常见的化归基本形式有：

1、数与数之间的转化。例如计算某个算式得出数值；化简某个解析式得出结果；变形所给出的方程求解；变形所给的不等式求出解集以及函数、方程、不等式之间的互相转化等等。

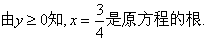
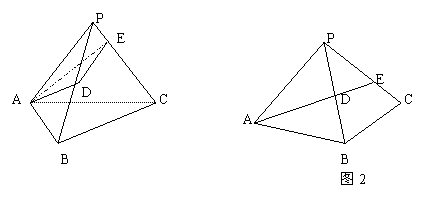
2、形与形之间的转化。比如：利用图象变换的知识作出函数图象；利用分割、补形、折叠、展开，作辅助线，辅助面处理空间图形或平面图形，等等。包括把立体问题化归为平面问题。

例2.如图，正三棱锥P-ABC中，各条棱的长都是2，E是侧棱PC的中点，D是侧棱PB上任一点，求△ADE的最小周长。

3、数与形之间的转化。数与形之间的转化主要是依据函数与其图象的关系；复数及其运算的几何意义；以及解析几何中曲线与方程的概念等等进行转化。

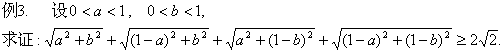
[分析]：这是含有四个无理式的不等式证明题，难以入手，可应用化归方法。注意到左边的四个无理式的结构与勾股定理相类似，由此想到，设法化归为几何问题。这容易得到化归一：构造如图3的正方形，可以说不等式关系不证自明。

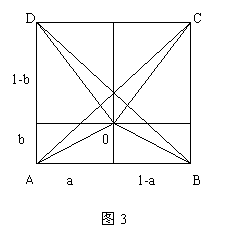
由此化归的思路，进一步考虑到两点间的距离这一关键，又可得到化归二：

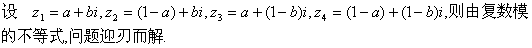
从第二种化归得到的解法，我们同时得出原问题的条件：

0<a<1，0<b<1是多余的，认识进一步深化。

4、实际问题与数学模型之间的转化。数学模型是从现实世界中抽象出来的，是对客观事物的某些属性的一个近似的反映，但对解决实际问题而言，数学模型却是深刻，正确、完善地反映着现实。因此，把所考察的实际问题，化归为数学问题，构造相应的数学模型，通过对数学模型的研究，使实际问题得以解决，充分地体现了"用数学"的意识和能力。比如以上所举的哥尼斯堡的七桥问题。

化归思想方法的主要特点是它的灵活性和多样性。一个数学问题，组成主要元素之间的相互依存和相互联系的形式是可变的，其形式并非唯一，而是多种多样。所以应用数学变换的方法去解决有关数学问题时，就没有一个统一的模式可以遵循。因此，我们必须根据问题本身提供的信息，利用动态的思维，具体问题具体分析，去寻求有利于问题解决的化归途径和方法。

在中学数学中，应用化归思想方法解题应注意三个点：

一.注意紧盯化归目标，保证化归的有效性、规范性

化归作为一种思想方法，应包括化归的对象、化归的目标、以及化归的方法、途径三个要素。因此，化归思想方法的实施应有明确的对象、设计好目标、选择好方法。而设计目标是问题的关键。设计化归目标时，总是以课本中那些基础知识、基本方法在应用上已形成固定的问题（通常称为规范性问题）为依据，而把要解决的问题化归为成规律问题（即a50问题的规范化）。化归能不能如期完成，与化归方法的选择有关，同时还要考虑到化归目标的设计与化归方法的可行性、有效性。因此，在解题过程中，始终必须紧紧盯住化归的目标，即始终应该考虑这样的问题：怎样才能达到解原问题的目的。在这个大前提下，实施的化归才是卓有成效的，盲目地选择化归的方向与方法必将走入死胡同。

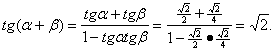
[说明]解题犹如打仗，需要冲破道道难关，直奔解题目标，而盯住目标，求什么就解什么，有助于最终形成解题思维链。

二.注意转化的等价性，保证逻辑上的正确

化归包括等价化归和非等价化归，在中学数学中的化归多为等价化归，等价化归要求转化过程中的前因后果既是充分的，又是必要的，以保证转化后的结果为原题的结果。

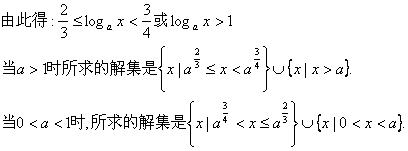
三、注意转化的多样性，设计合理的转化方案

在转化过程中，同一转化目标的达到，往往可能采取多种转化途径和方法。因此研究设计合理、简捷的转化途径是十分必要的，必须避免什么问题都死搬硬套，造成繁难不堪。

[说明]这个例子说明设计合理转化方案的重要性，目标的转换与方法转换是相辅相成又互相制约的，但其目的却是一致的，那就是通过化归达到以简驭繁的最终目的。

[说明]：本题体现了转化的多样性。最省、最多、最低、最大等最值问题，在现实生活中有着广泛的应用，在近年高考中，几乎年年都涉及到。此类问题，一般要构造函数，用函数值域、单调性、均值不等式、二次方程的判别式等数学方法求出最值。

以上的例题，从一个侧面体现化归思想方法在中学数学解题中的重要地位。利用化归思想解题时，转化的途径和方法不一定相同，但有一个共同的规律，就是在待解决的问题和已解问题之间架起一个联系的桥梁，这就是知识之间的"关系键"，这就要求我们在学习数学的过程中，要不断地构建知识结构，形成知识网络，要领悟蕴含在数学内容之中的数学思想方法，这些都是提高数学解题能力的条件和基础。

最后，还必须说明，化归思想是中学数学解题的重要思想方法，但并非万能的方法，即并不是所有的问题都可以通过化归而得到解决的。化归思想的成功应用是以"数学发现"为前提的。因此，我们不能只停留在化归的分析，而必须有创新的精神，不断地进行新的研究，在研究中获得新方法、新理论。

主要参考文献：

(1)殷堰工 《数学解题策略精编》 上海科技教育出版社 1994.7

(2)孙瑞清、熊斌等 《全国初中数学竞赛辅导》 北京大学出版社 1998.12

(3)黄文斐、徐凡等 《思维点拔与能力训练》 辽宁大学出版社 2000.7

(4)任志鸿等 《高考热点与冷点》 哈尔滨出版社 2001.2