提要 本文是"VB"环境下的算法教学探讨。文章通过四个实例揭示了如何将算法原理和程序框图转化为VB程序；如何借助VB程序上机实践来进一步理解算法的实质（二分法求近似根）；以及如何借助VB的循环语句解决较复杂的算法案例，从而深刻理解算法原理。本文还简要介绍了VB的基本语句，以此说明在"VB"环境下进行算法教学是符合数学课程与信息技术的整合中的"必要性"、"平衡性"、"广泛性"、"实践性"、"实效性"等原则。
主题词 VB 算法 教学
"现代信息技术的广泛应用正在对数学课程内容、数学教学、数学学习等方面产生深刻的影响。高中数学课程应提倡实现信息技术与课程内容的有机整合（如把算法融入到数学课程的各个相关部分），整合的基本原则是有利于学生认识数学的本质。"数学新课程标准关于"信息技术"的教学建议是：在教学中，应重视利用信息技术来呈现以往课堂教学中难以呈现的课程内容。同时，应尽可能使用科学型计算器、计算机及软件、互联网，以及各种数学教育技术平台，加强数学教学与信息技术的结合。数学新课程标准对算法内容的教学建议是：对算法内容，应着重强调使学生体会算法思想、提高逻辑思维能力，不应将算法简单处理成程序语言的学习和程序设计，同时应通过具体实例的上机实现（或编程）帮助学生理解算法思想及其作用。
新课程标准实验教科书《数学3》（必修，人教A版）对算法有如下描述："现代意义上的'算法'通常指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成"。算法实际上就是解决问题的一种程序性方法，它通常指向某一个或一类问题，而解决的过程是程序性和构造性的。用自然语言和程序框图来表示算法是可以的，但是用程序语言来表示算法和进一步认识算法仍然是必要的：一是为了解决某个具体问题，我们设计的算法包含大量烦琐的计算、复杂的作图等操作，这时计算机强大的数据处理功能可以帮我们轻松地完成这些重复性的机械步骤；二是"计算机解决任何问题都要依赖算法"，计算机解决问题的过程就是对算法的执行过程，但这个算法必须是计算机能理解的语言描述，而我们采取"VB"这种程序设计语言就是计算机可以理解的语言。"VB"是可视化的、面向对象的、采用事件驱动方式的结构化高级程序设计语言。我们可以轻松地画出用户界面，同时它的BASIC语言简单、易学，与教科书使用的类似BASIC的语句形式和语法规则能很好的融合，事实上办公软件EXCEL自带的VBA就是简单的"VB"程序设计语言。以下就从教科书的几个实例探讨如何进行算法教学。
一、用循环结构计算数列的前n项和
设计一个求12＋22＋32＋…＋1002的算法
分析：用循环结构解决本题．设累加变量为s，其初始值为0；计数变量为i，其值从1变到100．具体算法用程序框图表示如下：
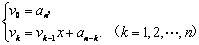
根据程序框图，我们直接用WHILE … WEND语句在"VB"下演示，学生能清楚的看到结果，同时可求任意项的和，体会算法的通用性。
Private Sub Form_Load()
Dim n As Long, s As Long
n = InputBox("请输入 n:", "从1到n求平方和", 100)
s = 0
i = 1
While i <= 100
s = s + i * i
i = i + 1
Wend
Show
Print "1 到 "; n; " 的平方和是："; s
End Sub
注：其和可以用公式n(n+1)(2n+1)/6验证。例如：
|
N |
10 |
50 |
100 |
1000 |
|
输出 |
385 |
15150 |
338350 |
333833500 |
二、用区间二分法求方程的近似解
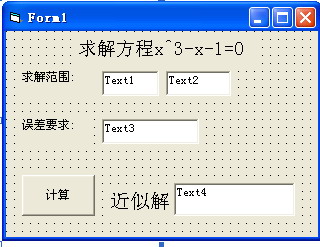
写出用区间二分法求方程x3-x-1=0在区间[1, 1.5]内的一个近似解（误差不超过0.0001）的一个算法。
分析：在"VB"环境下，只要画出界面，输入根据程序框图编写的程序代码，就能判断方程解的范围，计算出方程的近似解，在计算机上操作可以反复进行，有利于理解二分法的含义。
Private Sub Command1_Click()
a = Val(Text1.Text)
b = Val(Text2.Text)
e = Val(Text3.Text)
fa = (a * a - 1) * a - 1
fb = (b * b - 1) * b - 1
If fa * fb >= 0 Then
Text4.Text = "求解范围错！"
Else
Do
x = (a + b) / 2
f = (x * x - 1) * x - 1
If f * fa > 0 Then
a = x: fa = f
Else
b = x: fb = f
End If
Loop Until f = 0 Or Abs(b - a) < e
Text4.Text = Int(x / e + 0.5) * e
End If
End Sub
三、用秦九韶算法求多项式的值
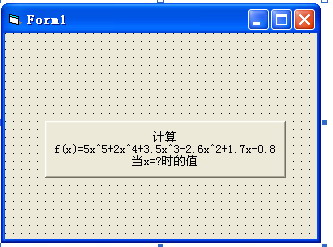
设计求多项式
当x=5时的值的秦九韶算法。
分析：秦九韶算法是求一元多项式的值的一种方法．我们把求f(x)=anxn＋an-1xn-1＋…＋a1x＋a0的值转化为求递推公式中vn的值．通过这种转化，把运算的次数由至多
次乘法运算和n次加法运算，减少为至多n次乘法运算和n次加法运算，大大提高了运算效率．因此，秦九韶算法是一个很好的算法，而这种用递推公式表示的步骤可以用循环结构来实现．对照教科书的程序框图，我们用"VB"实现如下：
Private Sub Command1_Click()
Dim C(10) As Double
x = InputBox("请输入求值数", "")
C(0) = -0.8: C(1) = 1.7: C(2) = -2.6: C(3) = 3.5: C(4) = 2: C(5) = 5
n = 1
v = C(5)
While n <= 5
v = v * x + C(5 - n)
n = n + 1
Wend
Print "所求的值是"; v
End Sub
Private Sub Command1_Click()
Dim C(10) As Double
For i = 0 To 5
C(i) = InputBox("输入x的i次幂系数", "")
Next i
x = InputBox("请输入求值数", "")
n = 1
v = C(5)
While n <= 5
v = v * x + C(5 - n)
n = n + 1
Wend
Print "所求的值是"; v
End Sub
四、用冒泡排序法进行排序
用冒泡排序法对8，3，2，5，9，6从小到大进行排序。
分析：在排序过程中，将两个相邻记录间的关键字进行比较，小者往上浮，大者往下沉，故称冒泡排序。其基本思想是从第一个记录开始，将每两个相邻记录之间的关键字进行比较。若不符合排序顺序，就交换这两个记录，直到第n个记录为止。第一次循环结束后，得到最大的记录。第二次循环仍重复上述步骤，直到 第n－1个记录，得到次大的记录。重复若干次后，便得到已排序好的一组记录。我们除了要理解这种日期计算器算法的基本思想，还应体会算法中的循环语句的应用。对教科书例题及习题可用下面算法（程序）实现。
Private Sub Command1_Click()
Dim C(10) As Double
For n = 1 To 6
C(n) = InputBox("输入需要排序的数", "6个数的冒泡排序", "")
Next n
For i = 1 To 6
For j = 6 To i Step -1
If C(j) < C(j - 1) Then a = C(j): C(j) = C(j - 1): C(j - 1) = a
Next j
Next i
For i = 1 To 6
Print "", C(i)
Next i
End Sub
事实上,我们只要掌握VB的几个简单语句,就可轻松地上机验证算法了.以下是VB的基本语句:
1．赋值语句:VB中的赋值运算符是"="，其一般格式如下：变量=值
2．输入函数InputBox :此函数用于将用户从键盘输入的数据作为函数的返回值返回到当前程序中。
3．输出函数MsgBox :MsgBox格式为：MsgBox(prompt[,buttons][,title][,helpfile,context])
4. 选择结构:
If 语句:(1)单行格式If语句：If 条件 Then 语句1 [Else 语句2];
(2)多行格式If语句:
If 条件 Then
语句体
End If
或If 条件 Then
语句体1
Else
语句体2
End If
或If 条件1 Then
语句体1
ElseIf 条件2 Then
语句体2
[ElseIf 条件3 Then
语句体3]
……
[Else
语句体n]
End If
5．循环结构:
For 循环变量 = 初始值 To 终值 [Step 步长]
[循环体]
[Exit For]
[循环体]
Next 循环变量
While循环的格式如下：
While 条件
[循环体]
Wend
Do循环的两种格式如下：
（1）格式一
Do
[语句体]
['满足某条件时
Exit Do]
[语句体]
Loop [While或Until 条件]
（2）格式二
Do [While或Until 条件]
[语句体]
['满足某条件时
Exit Do]
[语句体]
Loop
总之，在计算机环境下进行算法教学既是《课程标准》的要求，也是教师教学的愿望，更是学生学习的需要。在信息技术创设的数学学习环境中，操作、观察、试验、发现等过程变得具体而清晰，数学思维的目的性增强，数学推理的逻辑基础更加稳固，数学思考更具有程序性，这就增大了学生成功建构数学概念、解决数学问题的可能性，从而使以学生发展为本的教育理念得以实现。
参考文献:
1.人民教育出版社、课程教材研究所：《普通高中课程标准实验教科书（A版）
数学3》，人民教育出版社2004年5月第一版
2．中华人民共和国教育部：《普通高中数学课程标准（实验）》
本文获得"高中数学课程教材与信息技术整合的研究"课题子课题论文和优秀案例评比一等奖